This seminar is organized in partnership SPHERE / EHESS by Marc Chemillier (EHESS), Giovanna C. Cifoletti (EHESS), Sophie Desrosiers (EHESS) and Éric Vandendriessche (SPHERE, CNRS) :
https://enseignements-2016.ehess.fr...
PRESENTATION
During the seminar, we will present several cases of mathematical rationality: that which is manifested in the textile and musical creations, as well as in the practice of certain procedural activities (string games, drawings on the sand ...), but also those which are at the origin of certain disciplinary practices in mathematics, such as metrology and accounting in Mesopotamia or, for the European Renaissance, the dialectic in algebra and the practice of tables.
To current year
Archives : 2015–2016, 2014–2015, 2013–2014, 2012–2013
PROGRAM 2016–2017
Sessions at EHESS France (190-198 av de France 75013 Paris, then at EHESS 54 bd Raspail, 75006 Paris) on Wednesdays, 1 to 5 p.m., March 8th to June 7th.
March 8, March 22, April 26, May 10, May 17, May 24, June 07
March 8, Room 015, Ground0
- Sophie Desrosiers, Marc Chemillier, Giovanna Cifoletti & Éric Vandendriessche
Presentation of the seminar.
- Éric Vandendriessche (CNRS, SPHERE) & Céline Petit (SPHERE)
An introduction ethnomathematics.
:: Workshop "Weaving dualism in the Andes"
- A four-hour workshop hosted by Sophie Desrosiers
Instead of observing weaving practices, questioning the actors and analyzing their mathematical aspects, the participants will be led in the opposite step to know how to materialize through the selection of threads on a small loom the logic of dualism as practiced by weavers in the Andean highlands for more than two millennia. The material result is a strip without back with the same design on both sides and colors inverted.
April 26, !!!! Room BS1_05 (level-1), 54 bd Raspail 75006 Paris !!!!
:: Measuring time
- Bertrand Paoloni (doctorant, EHESS)
Mesure du temps et mécanique céleste. Quelques exemples de méridienne.
Contrairement aux cadrans solaires les plus répandus, les méridiennes sont des instruments de mesure du temps n’étant opérationnels qu’aux abords immédiats de midi. Durant la première modernité (XVIe et XVIIe siècle) ces installations ont joué un grand rôle dans la détermination de la durée de l’année et des dates de solstices et des équinoxes, permettant d’établir avec plus d’exactitude le calendrier des fêtes religieuses.
A travers l’étude de différents édifices (cathédrale de Florence, basilique de Bologne, église St-Sulpice à Paris...) nous verrons dans une première partie, comment ces instruments d’observation ont accompagné les principales découvertes de l’astronomie de l’époque. Nous tenterons de comprendre les enjeux scientifiques et religieux, qui ont poussé les astronomes à faire percer les dômes des églises afin de réaliser ces monumentaux cadrans solaires.
La seconde partie de notre intervention sera consacrée aux méridiennes du XVIIIe siècle. La popularité croissante des horloges et des montres entraîna le besoin d’une méthode plus précise d’indication du midi moyen. Grâce à une horlogerie plus ponctuelle, pour la première fois le public se rendit compte de l’irrégularité du mouvement du Soleil. Nous nous intéresserons à l’évolution des méridiennes et à leur fonction dans la prise de conscience de l’équation du temps.
References:- John L. Heilbron, Astronomie et églises, Paris, Belin, coll. « Pour la Science », 2003
- Andrée Gotteland, Les méridiennes du monde et leur histoire, t. I et II, Paris, Le Manuscrit, 2008
- Andrée Gotteland et Georges Camus, Cadrans solaires de Paris, Paris, CNRS, 1997
- Gerhard Dohrn-van Rossum, L’histoire de l’heure : L’horlogerie et l’organisation moderne du temps, Paris, La Maison des sciences de l’homme, 1997
- Jérôme Bonnin, La mesure du temps dans l’Antiquité, Paris, Les Belles Lettres, 2015
- David S. Landes, Revolution in Time. Clocks and the Making of the Modern World, Viking, 2000
- Denis Savoie, Cosmographie : Comprendre les mouvements du Soleil, de la Lune et des planètes, coll. « Pour la science », Paris, Belin, 2006
- Denis Savoie, La Gnomonique, Les Belles lettres, coll. « L’Âne d’or », vol. 17, Paris, 2007,
- Denis Savoie, L’aspect gnomonique de l’œuvre de Fouchy : La méridienne de temps moyen, Centre international de synthèse. Section d’histoire des sciences, CNRS (France), 2008
- Stéphanie Homola (CECMC/EHESS)
La fabrique des restes : une approche ethnomathématique des arts mantiques chinois.
Je présenterai mes recherches actuelles sur les pratiques et les textes relatifs à une forme de mnémotechnique de la main dans le monde chinois contemporain. Ce procédé, utilisé aujourd’hui dans des pratiques divinatoires et rituelles, consiste à s’aider de la paume de la main pour effectuer diverses opérations en parcourant avec le pouce les positions matérialisées par les phalanges des quatre autres doigts. A partir d’une ethnographie détaillée de techniques divinatoires pratiquées par des spécialistes mais aussi par l’homme du commun, ce travail propose d’étudier les opérations mentales à l’œuvre dans cette mnémotechnique, notamment les opérations de division ou de décompte dont l’objectif est de fabriquer des restes. Mises au regard de principes d’arithmétique modulaire, ces opérations seront analysées comme des processus cognitifs de simplification visant à rendre les informations divinatoires appréhendables par l’esprit humain.
References:- Daumas, Denis, Guillemot, Michel, Keller, Olivier, Mizrahi, Raphaël et Spiesser, Maryvonne. 2011. ‘Le Théorème des restes chinois : textes, commentaires et activités pour l’arithmétique au lycée. Toulouse : Institut de recherche sur l’enseignement des mathématiques, (en ligne) http://culturemath.ens.fr/materiaux/irem-toulouse11/theoreme-restes-chinois-index.html
- Hayek, Matthias. 2017. « Correlating Time within One’s Hand : The Use of Temporal Parameters in Early Modern Japanese "Chronomancy" Techniques ». In Michael Lackner (dir.), Coping With the Future. Theories and Practices of Divination in East Asia. Leiden : Brill (à paraître).
- Homola, Stéphanie. 2014. « Les usages de la main dans les calculs divinatoires ». Études chinoises, n° 33.1, p. 113-132.
- Homola, Stéphanie. 2015. « Ce que la main sait du destin : opérations et manipulations dans les pratiques divinatoires chinoises ». Ethnographiques.org, n° 31 « La part de la main » coordonné par Nicolas Adell et Sophie Chevalier, www.ethnographiques.org/2015/Homola
- Martzloff, Jean-Claude. 1988. Histoire des mathématiques chinoises. Paris : Masson.
May 10, !!!! Room BS1_05 (level-1), 54 bd Raspail 75006 Paris !!!!
:: (Ethno-)mathematics & artefacts - session 1
- Marc Chemillier (EHESS)
Graines et maths.
Les caillous qui forment l’étymologie du terme calcul (calculus = caillou en latin), les bouliers utilisés dans des régions aussi éloignées que la Chine, l’Inde et la Méditerranée, et les graines qui servent de support aux pratiques divinatoires à Madagascar, tous ces artefacts témoignent d’une pensée abstraite qui se développe en s’appuyant sur des objets concrets entretenant à des degrés divers un certain rapport avec le symbolisme utilisé en mathématiques.
References:- Le site Web SIKY Divination à Madagascar : http://ehess.modelisationsavoirs.fr/sikidy/index.html
- M. Chemillier, « Mathématiques de tradition orale », Math. Sci. hum., n° 178, 2007 (2), pp. 11-40: http://www.ehess.fr/revue-msh/pdf/N178R1265.pdf
- M. Chemillier, « Éléments pour une ethnomathématique de l’awélé », Math. Sci. hum, n° 181, 2008 (1), pp. 5-33 : http://msh.revues.org/docannexe9223.html
- J. Goody, La Raison graphique. La domestication de la pensée sauvage, Éditions de Minuit, 1979
- David Silva Labra (Doctorant, EHESS)
Résoudre une équation c’est comme équilibrer une balance ": artefact et imaginaire dans la résolution des équations.
Dans l’enseignement initial de l’algèbre, nous pouvons observer l’utilisation de l’image suivante : résoudre une équation c’est comme équilibrer une balance. Cette utilisation a été étudiée dans son aspect d’analogie/métaphore entre le concept mathématique d’équation et l’artefact « balance », mais aussi avec le lien que cette image fait entre une notion abstraite et l’expérience corporelle de l’équilibre (présente aussi dans la balance). Bien que l’on puisse noter certains avantages à ce type d’imaginaire (p. ex. l’ancrage corporel et culturel que la balance comporte), l’image en question peut présenter des problèmes, notamment par rapport à la représentation de la quantité soustractive et du nombre négatif dans l’artefact balance. En considérant que la liaison entre l’artefact balance et l’équation est déjà présente dans certaines traductions du texte de Al-Khwarizmi (p. ex. The Compendious Book on Calculation by Completion and Balancing) mais aussi chez d’autres auteurs pendant la réception et l’élaboration européenne de l’algèbre, on peut se poser les questions suivantes : comment la représentation de la quantité soustractive et nombre négatif a-t-elle été abordée dans le passé ? Le rapport entre la notion de balance et d’équation a-t-il changé dans le temps ? Cet imaginaire a-t-il toujours été présent dans la pratique de résolution des équations ? Par ces questions, nous cherchons à historiciser un phénomène abordé principalement par les sciences cognitives et de la didactique. Des éléments semblent indiquer que le rapport entre l’artefact balance et la notion d’équation est plus complexe et que l’on doit considérer les changements historiques dans la manière
References:- Johnson M., « Embodied Meaning and Cognitive Science », Language Beyond Postmodernism: Saying and Thinking in Gendlin’s Philosophy, Northwestern University Press, 1997.
- Lakoff G. et R.E. Núñez, Where mathematics comes from: how the embodied mind brings mathematics into being, New York, NY, Basic Books, 2000.
- Muḥammad ibn Mūsā al-Khwārizmī, The Compendious Book on Calculation by Completion and Balancing, traduit par Miriam T. Timpledon, traduit par Susan F. Marseken et traduit par Lambert M. Surhone, VDM Publishing, 2010.
- Otte M., « What is a Text? », B. Christiansen, A.G. Howson et M. Otte (dir.), Perspectives on Mathematics Education, Springer Netherlands, coll.« Mathematics Education Library », n˚ 2, 1986, p. 173-203.
- Steinbring H., « Do Mathematical Symbols Serve to Describe or Construct “Reality”? », M.H.G. Hoffmann, J. Lenhard et F. Seeger (dir.), Activity and Sign, Springer US, 2005, p. 91-104.
- Franck Jedrzejewski (CEA)
La raison diagrammatique.
Le diagramme n’est pas un concept nouveau mais il revêt selon les disciplines des sens et des fonctions différents. Au milieu du XXe siècle, les sciences mathématiques et physiques ont connu des bouleversements importants dans la façon de penser et de démontrer, si bien qu’il n’est pas illusoire de parler aujourd’hui, avec Penrose et Feynman, d’un tournant diagrammatique des sciences. Au cours de cette séance, nous nous efforcerons de montrer comment le diagramme, comme beaucoup de gestes figuratifs spontanés, restitue par un graphique ce que nous essayons de dire ou de penser, et livre des clés non triviales pour comprendre, par une dynamique qui lui est propre, la logique de conception d’un objet ou d’un phénomène quelconque. A travers la théorie des catégories de Samuel Eilenberg et Saunders MacLane, prélude à la théorie des noeuds et des entrelacs, nous montrons comment le diagramme a permis l’éclosion d’une technique plus générale que les mathématiciens appellent la catégorification. Fort de ces éléments, nous esquisserons la question d"un tournant diagrammatique en anthropologie.
May 17 mai, !!!! Room BS1_05 (level-1), 54 bd Raspail 75006 Paris !!!!
:: (Ethno-)mathematics & artefacts - session 2
- Sophie Desrosiers (EHESS, CRH)
Pratiques sociales du dualisme dans les Andes. [cont. of 3/22]
On verra comment la logique du dualisme qui se trouve au fondement du tissage dans certaines sociétés des hautes terres andines régit l’organisation des groupes sociaux et leurs relations avec et dans l’espace. La permanence de ces pratiques sur plus de deux millénaires pose la question du rôle de ces textiles comme mémoire matérielle d’idées fondamentales pour la survie de ces sociétés.
References:- Frame, Mary, "The Visual Images of Fabric Structures in Ancient Peruvian Art", in The Junius B. Bird Conference on Andean Textiles, ed. Ann P. Rowe, Washington, D.C., 1984, p. 47-80.
- Paul, Anne, "Color patterns on Paracas Necropolis weavings: a combinatorial language on ancient cloth", Techniques & culture, n° 29, 1997, p. 113-153.
- Desrosiers, Sophie, "El textil como matriz para el desarrollo de las artes plásticas en los Andes", Revista Española de Antropología Americana, n°43(2), 2013 : p. 477-514. Online: http://revistas.ucm.es/index.php/REAA/article/view/44020
- Desrosiers, Sophie, "Highland Complementary-Warp Weaving and the Lima Style in the Central Coast of Peru, ca. 200-650 C.E.". Textile Society of America Symposium Proceedings. Paper 917, 2014. http://digitalcommons.unl.edu/tsaconf/917
- Eric Vandendriessche (CNRS, SPHERE)
Elaborer/encoder/transmettre différentes formes de savoir dans la réalisation de figures de ficelle.
Nous verrons que les jeux de ficelle mélanésiens (Vanuatu, Papouasie-Nouvelle-Guinée) constituent/ constituaient un mode d’organisation et de transmission de certains savoirs (mythologiques, rituels…), impliquant l’usage de concepts mathématiques. Nous chercherons à mieux saisir en quoi cette pratique des jeux de ficelle pourrait être analysée comme une « technologie de la pensée » - sous un angle comparable à celui introduit par Jack Goody dans son analyse de l’écriture.
References:- Vandendriessche, E., 2012. Kaninikula, mathématiques aux îles Trobriand, film documentaire (26 min.), mars 2012, diffusion CNRS Images. http://videotheque.cnrs.fr/doc=4149?langue=FR
- Vandendriessche, E., 2014. Cultural and cognitive aspects of string figure-making in the Trobriand Islands, Journal de la société des Océanistes, n°138-139 (2014), p. 209-224.
- Vandendriessche, E., 2015. Ethnomathématique des jeux de ficelle trobriandais, ethnographiques.org, n°29 (2015). http://www.ethnographiques.org/2014/Vandendriessche
- Goody, J. (1979). La raison graphique. La domestication de la pensée sauvage. Paris, Minuit, « Le sens commun ».
- Roberto Casati (EHESS): discussant
May 24, 13:00–15:00 : Amphi François Furet, 15:00-17:00: salle 13, 6e étage, 105 bd Raspail, 75006 Paris
:: Ethnomathematics & training
- Jerry Lipka et David Koester (univ. Alaska Fairbanks, USA)
The mathematical principles behind everyday activities of Yupiaq elders and their potential implications for school mathematics
This long-term work, Math in a Cultural Context, arises from the close collaboration between Yupiaq cultural knowledge holders and university academics. We briefly describe how our group formed, how it functions, and the significance of having many years together, gaining deeper and more cogent insights. One surprising moment, out of many, stands out. That was when Mr. Jimmy, a ninety-two year old elder, explained that qukaq [the center] and ayagneq [a place to begin] the orthogonal center, was the center of everything. He literally meant that this cultural concept, which he expressed with crossed index fingers, was fundamental to their ways of thinking as they perform a wide array of activities from making patterns to navigating by the stars. Symmetry, measuring as a comparison-of-quantities, halving, folding algorithms, and physical verifications of equality and/or congruence are the associated mathematical principles that support everyday activities. We explore how teaching and learning mathematics can arise from these principles.
References:- Jerry Lipka. “Toward a Culturally Based Pedagogy: A Case Study of One Yup’ik Eskimo Teacher”. Anthropology & Education Quarterly, Vol. 22, No. 3 (Sep., 1991), pp. 203-223
- Jerry Lipka, Barbara L. Adams, Anthony Rickard, Dora Andrew-Ihrke, Eva Evelyn Yanez, and Ann Millard. “The Potential of a Culturally Based Supplemental Mathematics Curriculum to Improve the Mathematics Performance of Alaska Native and Other Students”. Journal for Research in Mathematics Education, 2012, Vol. 43, n°1, pp. 75-113.
- Catherine Sophian. The origins of mathematical knowledge in childhood. Mahwah, N.J.: Erlbaum, 2007.
- Paul Lockhart. Measurement. Harvard University Press, 2012
- Rik Pinxten (univ. de Ghent, Belgique) et Karen François (Free University Brussels, VUB)
Multimathemacy: Time to reset?
This presentation criticizes the current mathematics curriculum and the cultural biased dropout as a result of it. We analyse the inequality of the school system and the cultural biased dropout based on philosophical and empirical evidence. At the philosophical level, evidence is shown by relying on the work of mathematician and philosopher A.N. Whitehead and contemporary theoretical insights on (mathematics) education. Empirical evidence for our argument is given by the analysis of the international PISA 2012 figures and empirical research at the national level of the Belgium/Brussels school system(s). Based on our own experience, our research and teaching practice, we will give some good practices to illustrate our concept of multimathemacy and to provide an idea of how to reset the curriculum.
References:- Pinxten, R. & François, K. (2011). Politics in an Indian canyon? Some thoughts on the implications of ethnomathematics. Educational Studies in Mathematics, n°78 (2): 261-273.
- François, K. & Pinxten, R. (upcoming). Multimathemacy: Time to reset? Paper accepted for the MES-9 “Mathematics Education and Society”, 9th International Conference, Greece, Volos, 7–12 April 2017.
June 7, 13:00–17:00, salle 13, 6e étage, 105 bd Raspail, 75006 Paris
:: The drawings on the sand
- Introduction by Marc Chemillier & Eric Vandendriessche
- Alban Da Silva (ESPE, Univ. de Nouvelle Calédonie)
Ethnomathématique des dessins sur le sable de Vanuatu.
Ethnomathématique des dessins sur le sable de Vanuatu.
La pratique du « dessin sur le sable » a pu être observée depuis les années 1930 dans diverses aires culturelles, notamment dans des sociétés de tradition orale du Vanuatu (ex Nouvelles-Hébrides). Cette activité consiste à tracer une ligne continue avec le doigt, sur un sol de sable ou de cendre, en réalisant un dessin (le plus souvent) symétrique. Je montrerai dans un premier temps que des travaux issus de l’anthropologie (Deacon & Wedgwood 1934, Rowe 1936) permettent d’établir des « règles » géométriques auxquelles semble obéir cette pratique, ce qui permet d’en interroger la rationalité mathématique. A cet effet j’exposerai, dans un second temps, une analyse ethnomathématique qui permet de mettre au jour certains invariants procéduraux et algorithmiques. Enfin, je présenterai des opérations élémentaires de concaténation et de « couper/coller » qui permettent de faire des hypothèses sur les processus de création de certains dessins, tout en donnant des perspectives méthodologiques pour un travail de terrain.
References:- Ascher, M. (1994). Ethnomathematics: A multicultural view of mathematical ideas. CRC Press.
- Ascher, M. (1988). "Graphs in Cultures: A Study in Ethnomathematics". Historia Mathematica, n°15: 201-227.
- Deacon, A. B., & Wedgwood, C. H. (1934). "Geometrical drawings from Malekula and other islands of the New Hebrides". Journal of the Royal Anthropological Institute of Great Britain and Ireland, n°64, 129-175.
- Rowe, W. P. (1936). "A study of the geometrical drawings from the New Hebrides". Journal of the Royal Anthropological Institute of Great Britain and Ireland, n°66, 117-128.
- Jean-Paul Allouche (UPMC)
Un kolam indien et la suite de Thue-Morse.
On trouve en Inde, mais aussi dans d’autres pays, le « kolam » représenté à gauche dans la figure ci-dessous.
En itérant cette construction, on obtient les autres dessins de cette même figure.
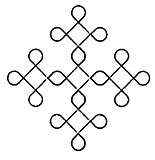 |
 |
 |
Comment dessiner simplement cette courbe et la courbe « à la Sierpinski » qu’on obtient après une infinité d’itérations ?
C’est ce que nous expliquerons en établissant un lien avec une suite binaire « automatique » bien connue, la suite de Prouhet-Thue-Morse :
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 …
References:
- G. Allouche, J.-P. Allouche, J. Shallit, "Kolam indiens, dessins sur le sable aux îles Vanuatu, courbe de Sierpinski et morphismes de monoïde", Annales de l’Institut Fourier, 56 (2006), 2115-2130.
- M. Chemillier, Les mathématiques naturelles, Odile Jacob, 2007



